Lingkaran adalah sebuah bentuk yang dibatasi oleh satu garis lengkung dengan jarak dari titik tertentu. Unsur dalam lingkaran antara lain berupa jari-jari, busur, dan juring. Dengan menggunakan rumus yang berlaku kita dapat menghitung luas yang ada pada bidang tersebut tersebut. Untuk memudahkan dalam menghitung luas lingkaran, berikut ini kami bagikan cara memecahkan soal perhitungan dengan sederhana dan cepat. Ulasan dilengkapi dengan rumus lingkaran beserta contoh-contoh soal dan pembahasannya.
Selamat berhitung!
Unsur – Unsur Lingkaran
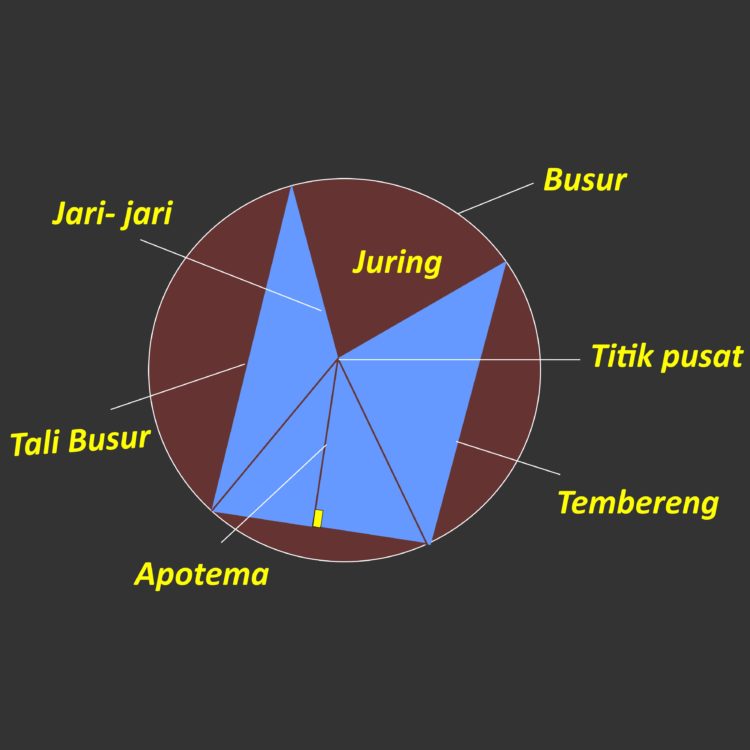
Lingkaran adalah salah satu bangun datar dua dimensi yang sering dijumpai dalam perhitungan soal matematika semenjak kita di TK bahkan Paud sekalipun.
Namun, sebelum beranjak untuk berlatih memecahkan soal mencari luas lingkaran, yuk pelajari unsur- unsurnya!
Agar lebih mudah untuk memahaminya, jangan lupa disimak gambar lingkaran di bawah ini ya!
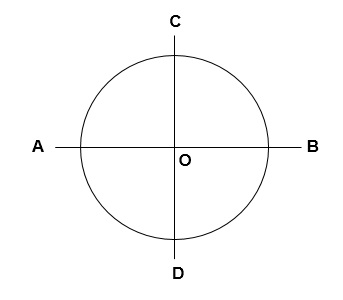
Diameter
Dalam lingkaran, diameter adalah panjang garis lurus yang akan menghubungkan antara kedua titik pada keliling lingkaran yang melalui pusat lingkaran.
Sesuai dengan pengertian ini, sederhananya diameter adalah dua kali dari jari- jari lingkaran.
Nah, sudah paham kan ya? Pada gambar diatas, diameter adalah pasangan huruf AB dan CD.
Jari- Jari
Di dalam lingkaran, jari- jari diiibaratkan seperti jeruji pada roda.
Jeruji- jeruji ini yang nantinya akan terhubung secara terpusat pada titik roda.
Nah, sehingga sederhananya asal usul jari- jari adalah setengah dari diameter lingkaran.
Lebih gampangnya, jari- jari adalah garis AO, OB, CO dan DO
Titik Pusat
Selain memahami diameter dan jari- jari- jari, maka selanjutnya adalah titik pusat.
Titik pusat adalah titik sentral yang terletak tepat di tengah lingkaran.
Pada gambar diatas, yang dimaksud titik pusat adalah huruf O.
Busur
Busur yang terdapat pada lingkaran mudah dikenali dengan melihat garis lengkung pada lingkaran.
Busur sendiri dalam lingkaran terdiri dari dua jenis, yakni busur besar dan busur kecil.
Maksud busur besar yakni ukuran panjangnya lebih dari setengah lingkaran.
Sedangkan untuk busur kecil sendiri, panjangnya kurang dari setengah lingkaran.
Jika diperhatikan secara seksama pada gambar, garis lengkung adalah garis AC, CB, BD dan DA.
Tali Busur
Tali busur pada lingkaran merupakan sebuah garis lurus yang mengkoneksikan dua titik pada keliling lingkaran dan bukan melalui titik pusat lingkaran.
Jika dianalogikan, tali busur mudah sekali untuk dikenali dengan benda di sekitar kita, misalnya busur panah.
Tembereng
Makna tembereng pada bentuk datar lingkaran merupakan daerah yang terletak di dalam lingkaran dan dibatasi oleh busur dan tali busur lingkaran.
Apotema
Selanjutnya, salah satu yang merupakan unsur dari lingkaran adalah apotema lingkaran.
Apotema sendiri dimaknai seperti jarak yang paling pendek antara tali busur dan titik pusat lingkaran.
Biasanya, garis ini bersifat tegak lurus dengan tali busur.
Juring
Juring adalah bagian yang diberi batasan oleh kedua garis jari- jari dan dibatasi busur lingkaran yang dihimpit oleh dua jari- jari. Juring sendiri terdiri dari dua jenis, yakni juring besar dan juring kecil.
Sudut Keliling
Sudut keliling pada lingkaran adalah sudut yang terjadi atau terbentuk dikarenakan adanya pertemuan antara dua tali busur melalui satu titik pada keliling lingkaran.
Sudut Pusat
Sudut pusat adalah sudut yang terjadi karena adanya perpotongan diantara dua jari- jari pada titik pusat lingkaran.
Rumus Lingkaran
Di dalam pembelajaran materi bentuk datar, tidak dapat dinafikkan bahwasannya setiap bangun datar punya perhitungan rumus masing- masing.
Rumus ini juga yang perlu dipelajari, supaya nanti soal- soal dapat dipecahkan dengan mudah!
Di dalam lingkaran, poin penting yang perlu diingat yakni jari- jari (r) dan π (baca : phi).
Nilai dari “phi” adalah atau 3.14 dan nilai tersebut tidak dapat dirubah dan bersifat tetap.
Pun, penggunaan phi dalam rumus berdasarkan koefisien dari jari- jari.
Sederhananya, penggunaan phi dengan nilai 3.14 bisa digunakan dengan jari- jari (r) yang berupa angka asli manapun selain kelipatan 7 maupun angka yang bersifat desimal.
Sedangkan, untuk penggunaan dapat digunakan pada angka dengan kelipatan 7.
Berikut rumus dari luas lingkaran :
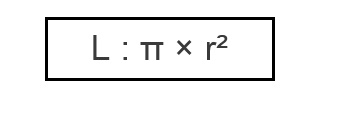
Contoh Soal Luas Lingkaran
Tingkat Dasar
Setelah memahami unsur dan rumus lingkaran diatas, maka pemahamannya perlu ditingkatkan dengan mengenali berbagai versi soal baik dalam bentuk cerita maupun gambar bangun datarnya.
Nah, berikut ada beberapa contoh soal perhitungan matematika tingkat dasar yang bisa dicoba untuk ananda di rumah bersama keluarga.
Soal Menghitung Luas Lingkaran Penuh
a. Rena merencanakan akan membuat taman dengan bentuk lingkaran di tanah lapang depan rumahnya.
Arsitektur taman mengusulkan agar diameter tamannya sebesar 28 cm.
Kira- kira berapakah luas taman Rena nanti?
Pembahasan :
Diameter/ d : 28 cm
Jari – jari/ r : 14 cm
π : 227
Luas?
L = π × r²
= 227 x 142
= 227 x 256
= 804. 57
Jadi, luas taman Rena yang berbentuk lingkaran sebesar 804.57 cm2
b. Perhatikan contoh soal di bawah ini!
Bibah menyimpan roda sepeda mainannya di kamar.
Bibah ingin belajar untuk mencari luas dari roda tersebut.
Kira- kira berapakah luasnya kalau jari- jari roda tersebut adalah 8 cm?
Ayo bantu Bibah menghitung luas rodanya!
Pembahasan :
Jari – jari/ r : 8 cm
π : 3.14
Luas?
L = π × r²
= 3.14 x 82
= 3.14 x 64
= 200.96
Jadi luas roda mainan Bibah adalah 200.96 cm2
Soal Menghitung Luas Setengah Lingkaran
a. Suatu hari, ibu pergi ke Pasar Krempyeng untuk membeli sayur dan kembaliannya diberi kerupuk Opak.
Bentuk kerupuk Opak berbentuk lingkaran dengan diameter 20 cm.
Namun, sesampainya di rumah, kerupuk tersebut diminta oleh kedua anaknya.
Akhirnya, ibu memberi keduanya anaknya dengan memotong kerupuk tersebut menjadi dua bagian sama rata.
Kira- kira berapakah kerupuk yang didapatkan masing- masing?
Pembahasan :
Diameter : 20 cm
Jari – jari/ r : x d = 10 cm
π : 3.14
Luas?
L = π × r²
= 3.14 x 102
= 314
Jadi luas roda mainan Bibah adalah 314 cm2
b. Adekha diberikan tugas oleh guru matematikanya.
Namun, Adekha kesulitan untuk menyelesaikannya.
Bantu Adekha untuk menemukan jawabannya dengan memperhatikan gambar di bawah ini!
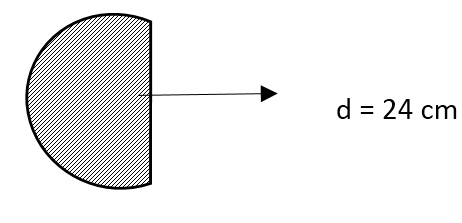
Berapakah luas dari gambar yang diarsir?
Pembahasan :
Diameter (d) : 24 cm
Jari – jari (r) : 12 cm
π : 3.14
Luas yang diarsir = Luas lingkaran
L = 1/2 x π × r²
= 1/2 x 3.14 x 122
= 1/2 x 3.14 x 144
= 226.08
Jadi, luas dari area yang diarsir adalah 226.08 cm2
b. Sebagai guru matematika, Pak Dana memiliki alat peraga untuk menunjukkan sebuah lingkaran.
Lingkaran itu mempunyai diameter sepanjang 28 cm.
Berapa kira- kira luas setengah lingkaran dari alat peraga Pak Dana?
Pembahasan :
Diameter (D) : 28 cm
Jari – jari (r) : 14 cm
π : 22/7
Luas lingkaran = 1/2 x π × r²
= 1/2x 22/7 x142
= 1/2x 22/7 x 256
= 402.28
Jadi, luas setengah lingkaran dari alat peraga Pak Dana adalah 402.28 cm2
Soal Menghitung Seperempat Lingkaran
a. Andi ingin membagi kue bolunya yang beralas lingkaran sempurna dengan Dina, Dani dan Dena.
Sehingga masing- masing akan mendapat bagian. Kira- kira berapa bagian yang didapatkan masing- masing?
Pembahasan :
Diameter (d) : 49 cm
Jari – jari (r) : 24.5 cm
π : 3.14
Luas yang diarsir?
Luas lingkaran = 1/4 x π × r²
= 1/4 x 3.14 x 24.52
= 1/4 x 3.14 x 600.25
= 471.19
Jadi luas area lingkaran adalah 471.19 cm2
b. Perhatikan contoh soal dengan seksama!
Rena dan Ririn mendapatkan pekerjaan rumah matematika dari Pak Yana.
Rena kebingungan bagaimana menghitung luas dari seperempat lingkaran.
Bagaimana seharusnya cara menghitung luas benda yang diarsir?
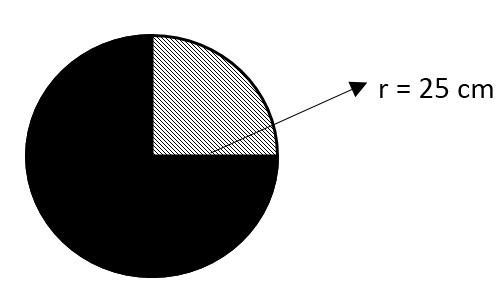
Pembahasan :
Jari – jari (r) : 25 cm
π : 3.14
Luas yang diarsir?
Luas lingkaran = 14 x π × r²
= 1/4 x 3.14 x 252
= 1/4 x 3.14 x 625
= 490.625
Jadi luas area seperempat lingkaran adalah 490.625 cm2
Soal Menghitung Sepertiga Lingkaran
a. Ibu ingin membagi sama rata kue bolu yang berbentuk lingkaran saat berbelanja ke pasar kepada Indri, Ari dan Shila.
Berapa bagian yang didapat oleh ketiga anak ini?
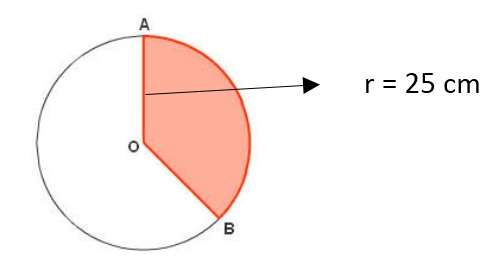
Pembahasan :
Jari – jari (r) : 25 cm
π : 3.14
Luas yang diarsir?
Luas lingkaran = 1/3 x π × r²
= 1/3 x 3.14 x 252
= 1/3 x 3.14 x 625
= 654.1
Jadi, masing- masing anak Ibu akan mendapatkan jatah kue sebesar 654.1 cm2
b. Perhatikan dengan seksama soal cerita berikut!
Dila dan Sasa akan membagi rata luas tanahnya yang berbentuk lingkaran kepada ketiga sepupunya.
Diameter tanah yang dimiliki oleh Dila dan Sasa yakni 65 cm2.
Kira- kira berapa luas lingkaran yang didapatkan ketiga sepupunya?
Pembahasan :
Diameter (d) : 65 cm
Jari – jari (r) : 32.5 cm
π : 3.14
Luas yang diarsir?
Luas lingkaran = 1/3 x π × r²
= 1/3 x 3.14 x 32.52
= 1/3 x 3.14 x 1056.25
= 1105.541
Jadi luas tanah masing- masing yang didapatkan sebesar 1105.541 cm2
Tingkat Lanjut
Nah, berikut ada contoh berbagai soal untuk yang sudah ada di tingkat lanjut ya, misal level SMP maupun SMA.
Biasanya, di level ini tingkatan soal sudah semakin sulit. Jadi, jangan lupa teliti dalam memahami soal ya!
Soal Menghitung Luas Lingkaran dalam Persegi
a. Perhatikan gambar diatas, berapakah luas daerah yang diarsir dan tidak diarsir?
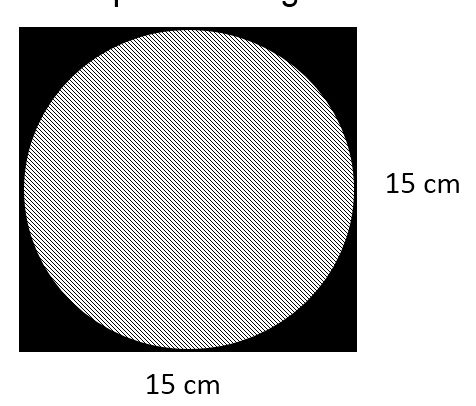
Pembahasan :
Luas daerah yang diarsir : Luas lingkaran
Luas daerah yang tidak diarsir : Luas Persegi
Sisi (s) : 15 cm
Diameter (d) : 15 cm
Jari – jari (r) : 7.5 cm
π : 3.14
Luas yang diarsir?
Luas lingkaran = π × r²
= 3.14 x 7.52
= 3.14 x 56.25
= 176.625
Luas yang tidak diarsir?
Luas yang tidak diarsir = Luas Persegi – Luas Lingkaran
= (s x s) – (π × r²)
= (15 x 15) – 176.625
= 225 – 176.25
= 48.75
Jadi luas daerah yang diarsir adalah 176.625 cm2 dan luas yang tidak diarsir adalah 48.75 cm2
b. Perhatikan dengan teliti gambar di bawah ini!
Berapakah luas daerah yang diarsir dan luas daerah secara keseluruhan?
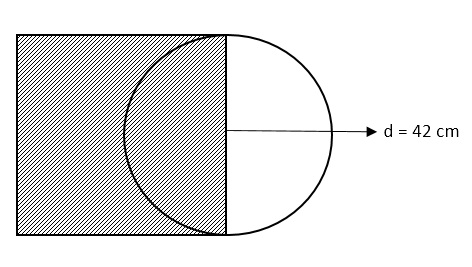
Pembahasan :
Luas daerah yang diarsir = Luas Persegi
Luas Keseluruhan = Luas Persegi + Luas 1/2 Lingkaran
Sisi (s) : 42 cm
Diameter (d) : 42 cm
Jari – jari (r) : 21 cm
π : 3.14
Luas daerah yang diarsir (luas persegi) = s x s
= 42 x 42
= 1764
Luas Keseluruhan = Luas Persegi + Luas 1/2 Lingkaran
= 1764 + ( 1/2x π × r²)
= 1764 + ( 1/2 x 3.14 x 21²)
= 1764 + ( 1/2 x 3.14 x 21²)
= 2456.37
Jadi, luas daerah yang diarsir adalah 1764 cm2 dan luas secara keseluruhan adalah 2456.37 cm2.
Soal Menghitung Luas Lingkaran dalam Segitiga
a. Perhatikan gambar diatas dan carilah luas area yang diarsir!
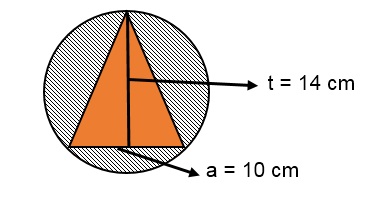
Pembahasan :
Luas area yang diarsir : Luas Lingkaran – Luas Segitiga
Alas (a) : 10 cm
Diameter (d) = Tinggi (t) : 14 cm
Jari – jari (r) : 7 cm
π : 227
Luas area yang diarsir = Luas Lingkaran – Luas Segitiga
= ( π × r²) – (12 x a x t)
= (227 × 7²) – (12 x 10 x 7)
= (227 × 49) – (12 x 70)
= 154 – 35
= 119
Jadi, luas area yang diarsir adalah 119 cm2
Soal Menghitung Luas Lingkaran luar Segitiga
a. Kerjakan dengan seksama soal di bawah ini dan hitunglah :
Luas area yang diarsir.
Luas area yang tidak diarsir.
Luas area secara keseluruhan.
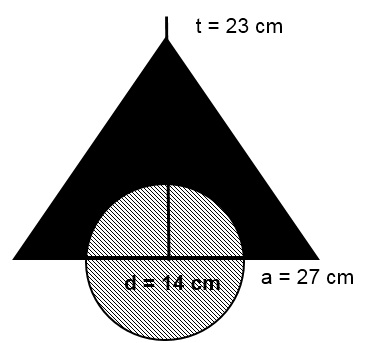
Pembahasan :
Alas (a) : 27 cm
Diameter (d) : 14 cm
Tinggi (t) : 23 cm
Jari – jari (r) : 7 cm
π : 227
Luas area yang diarsir = Luas Lingkaran
Luas lingkaran = π × r²
= 227 × 7²
= 227 × 49
= 154
Luas area yang tidak diarsir = Luas Segitiga – Luas 1/2 Lingkaran
= (1/2 x a x t) – (12x π × r²)
= ( 1/2 x 27 x 23) – ( 12 x 227x 7²)
= ( 1/2 x 621 ) – ( 12 x 154)
= 310.5 – 77
= 233.5
Luas Secara keseluruhan = Luas Segitiga + 1/2 Lingkaran
= (1/2 x a x t) – (1/2x π × r²)
= ( 1/2 x 27 x 23) + ( 1/2 x 227x 7²)
= ( 1/2 x 621 ) + ( 1/2 x 154)
= 310.5 + 77
= 387.5
Jadi, luas permukaan area yang diarsir adalah 154 cm2, sedangkan luas area yang tidak diarsir adalah 233.5 cm2 dan total luas secara keseluruhan adalah 387.5 cm2.
Soal Menghitung Luas Penampang Lingkaran
a. Perhatikan contoh soal berikut ini!
Sebuah mobil memiliki penampang pada masing- masing rodanya berbentuk lingkaran dengan jari- jari sebesar 40 cm.
Kira- kira berapa luasnya dalam satuan m2 untuk penampang pada seluruh mobil tersebut?
Pembahasan :
Langkah pertama, ubah satuan cm menjadi satuan meter.
40 cm = 0.4 m
Luas satu penampang
L= π × r²
= 3.14 x 10²
= 314
Karena penampang ada 4, maka luas roda akan dikalikan sebanyak 4 untuk diketahui jawabannya.
L. Penampang = 4 x 314
= 1256
Jadi, luas keseluruhan penampang adalah 1256 m2.
Nah, itu tadi beberapa contoh soal yang akan menemani ananda belajar di rumah.
Pastikan untuk membaca dan melakukan pembuktian secara mandiri dnegan jawaban yang sudah tersedia!
Selain menggunakan perhitungan manual, ada banyak juga aplikasi yang dapat digunakan untuk menghitung luas lingkaran dengan penggunaan coding integral, flowchart bahkan algoritma.
Namun, di artikel kali ini, pembahasan akan dicukupkan untuk belajar menghitung luas lingkaran secara manual dahulu ya.
Kalau sudah mahir hitungan secara manual, nanti akan dibahas program perhitungannya. Tetap sukses dan semangat!
