Matematika dasar adalah kunci dari pemahaman menyeluruh mata pelajaran berhitung.
Setelah mempelajari bilangan, pemahaman selanjutnya adalah pada suatu pokok bahasan yaitu bilangan prima.
Meskipun termasuk level dasar, jika tidak mengulasnya secara detail tentunya materi bilangan prima ini akan sulit dipahami.
Untuk itu, mari kita pelajari lebih mendalam apa saja sih yang perlu kita ketahui dari materi bilangan prima ini.
Pengertian Dan Kegunaan Bilangan Prima

Sebelum memasuki pembahasan bilangan prima, tentunya kita sudah mengetahui makna atau arti dari bilangan dan bilangan asli kan?
Ya benar, bilangan adalah suatu konsep di dalam matematika yang digunakan sebagai alat penghitung.
Jika diurutkan dari kiri ke kanan akan membentuk kumpulan angka yang mewakili nilai satuan, puluhan, hingga tak terhingga.
Sedangkan, bilangan asli adalah bilangan bulat yang sudah sering kita temui di kehidupan kita sehari-hari yaitu angka 1,2, 3, 4 dst hingga tak hingga, termasuk angka 0 (nol).
Sepertinya dua pengertian ini sudah secara sadar kita mengerti ya.
Bilangan prima adalah bilangan asli yang dapat dibagi oleh bilangan itu sendiri dan dapat pula dibagi dengan angka 1.
Atau bahasa kerennya begini ni, bilangan prima adalah bilangan asli yang hanya memiliki dua faktor bulat positif.
Jadi, bilangan prima ini ada diantara deretan bilangan asli yaitu di antara 1 dan angka seterusnya.
Sebagai pengingat, angka 1 tidak termasuk ke dalam bilangan prima ya.
Mengapa? Karena 1 tidak memenuhi syarat menjadi bilangan prima.
Angka 1 hanya memenuhi 1 syarat menjadi bilangan prima, yaitu dibagi oleh bilangan itu sendiri.
Lalu, yang dimaksud bilangan prima adalah angka yang dimulai setelah 1.
Apa saja? Contohnya adalah angka 2. Angka ini dapat dibagi dengan 2 dan juga 1.
Contoh bilangan prima antara 1–10 adalah 2, 3, 5 dan 7.
Sekarang kita telah memahami arti dari bilangan prima, lalu apa sih kegunaannya?
Ternyata banyak sekali kegunaan dari bilangan prima ini.
Berikut penjelasannya.
Berguna dalam menjalankan fungsi Faktor Persekutuan Terbesar (FPB) dan Faktor Persekutuan Terkecil (KPK).
Sebagai contoh, untuk menyederhanakan pecahan 15/35, kita dapat menggunakan bilangan prima dengan FPB. Angka 35 dan 15 FPB-nya adalah 5.
Maka pecahan 15/35 dapat diperkecil menjadi pecahan 3/7.
Contoh lain, Kakak mempunyai 12 roti dan 8 es krim yang akan dibagikan pada adik-adiknya yang berjumlah 4 orang. Bagaimana pembagiannya? 8 dan 12 mempunyai FPB yaitu 4.
Jumlah roti dan es krim yang di dapat setiap adik adalah dicari dengan cara membagi 12 dan 8 dengan 4.
Maka setiap adik akan mendapatkan 3 roti dan 2 es krim.
Dalam hal KPK, biasanya bilangan prima ini digunakan untuk menyelesaikan masalah yang berkaitan dengan waktu temu.
Misal, Rama membeli apel di toko X setiap 7 hari sekali, Deden membeli apel di toko X setiap 3 hari sekali dan Pandu membeli apel di toko X setiap 4 hari sekali.
Di hari keberapa mereka akan berjumpa di toko X untuk membeli apel? Jawabannya adalah hari ke 84 karena KPK dari 7, 4 dan 3 adalah 84.
Bilangan prima juga sangat berguna untuk teknologi.
Ternyata bilangan ini dapat menjadi unsur pembentuk enkripsi di sistem komputasi.
Ini berkaitan dengan keamanan jaringan internet.
Peran bilangan prima disini adalah menjadi dasar pembuat kunci dan algoritma pengamanannya.
Ilmu yang mempelajari ini adalah ilmu kriptografi (cryptography).
Penerapan lebih lanjut dari bilangan prima adalah untuk sistem pengamanan rekening bank.
Sangat menarik bukan. Inilah pentingnya kita mempelajari dan memahami pokok bahasan bilangan prima ini.
Contoh Bilangan Prima
a. Bilangan Prima 1-10
Antara angka 1-10, hanya terdapat 4 bilangan prima yaitu 2, 3, 5 dan 7.
Kombinasi 1 huruf genap dan ganjil ini sangat mudah untuk dihafalkan.
Mereka juga sering muncul.
Untuk lebih mudah menghafalnya, kita bisa mengingatnya dengan melafalkan singkatan seperti : dugamaju, yaitu dua tiga lima tujuh.
Perlu diingat bahwa angka 2 adalah satu-satunya bilangan prima yang merupakan bilangan genap.
b. Bilangan Prima 1-100
Pada rentang ini, bilangan prima yang terbentuk adalah 25 angka.
Di bawah ini adalah daftar tersebut.
| 2 | 3 | 5 | 7 | 11 |
| 13 | 17 | 19 | 23 | 29 |
| 31 | 37 | 41 | 43 | 47 |
| 53 | 59 | 61 | 67 | 71 |
| 73 | 79 | 83 | 89 | 97 |
c. Bilangan Prima 1-1000
Ada 168 bilangan prima di antara rentang angka 1-1000.
Berikut himpunan dari angka-angka tersebut.
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 |
| 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 | 71 |
| 73 | 79 | 83 | 89 | 97 | 101 | 103 | 107 | 109 | 113 |
| 127 | 131 | 137 | 139 | 149 | 151 | 157 | 163 | 167 | 173 |
| 179 | 181 | 191 | 193 | 197 | 199 | 211 | 223 | 227 | 229 |
| 233 | 239 | 241 | 251 | 257 | 263 | 269 | 271 | 277 | 281 |
| 283 | 293 | 307 | 311 | 313 | 317 | 331 | 337 | 347 | 349 |
| 353 | 359 | 367 | 373 | 379 | 383 | 389 | 397 | 401 | 409 |
| 419 | 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 | 463 |
| 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 | 523 | 541 |
| 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 | 599 | 601 |
| 607 | 613 | 617 | 619 | 631 | 641 | 643 | 647 | 653 | 659 |
| 661 | 673 | 677 | 683 | 691 | 701 | 709 | 719 | 727 | 733 |
| 739 | 743 | 751 | 757 | 761 | 769 | 773 | 787 | 797 | 809 |
| 811 | 821 | 823 | 827 | 829 | 839 | 853 | 857 | 859 | 863 |
| 877 | 881 | 883 | 887 | 907 | 911 | 919 | 929 | 937 | 941 |
| 947 | 953 | 967 | 971 | 977 | 983 | 991 | 997 |
Namun, jangan khawatir.
Ternyata ada rumus dan cara mudah untuk mencari bilangan prima.
Faktor Prima Dan Pohon Faktor
Bagai pinang dibelah dua. Inilah istilah yang tepat untuk menandai faktor prima dan pohon faktor.
Pasalnya, kedua istilah ini benar-benar saling berdekatan, sehingga pengertiannya menjadi saling terikat satu dengan yang lain.
Faktor prima adalah bilangan prima yang digunakan untuk membagi suatu bilangan.
Bentuk pembagian terhadap bilangan ini biasanya disusun ke bawah.
Bilangan yang dibagi diletakkan paling atas, lalu di sebelah kiri bawah dari bilangan yang dibagi tersebut diletakkanlah bilangan prima (pembagi yang sering disebut ‘faktor’) dan di sisi kanannya adalah hasil baginya.
Sehingga bentuk ini menyerupai pucuk pohon.
Nah inilah yang mendasari pengertian dari pohon faktor.
Singkatnya, pohon faktor adalah bagan berbentuk pohon yang merupakan penjabaran dari hasil kali suatu bilangan dengan bilangan prima.
Bingung? Nah coba kita kerjakan soal di bawah ini.
Angka 70, apa saja faktor primanya?
Jawab : untuk mendapatkan faktor prima dari soal di atas kita harus membagi bilangan 70 dengan bilangan prima, coba mulai dari yang terkecil, yaitu 2.
Ternyata bisa, maka 70 : 2 adalah 35.
Selanjutnya 35 kita bagai lagi dengan bilangan prima lain, jika masih bisa.
Ternyata bisa dibagi 5.
Sehingga 35 : 5 adalah 7. Angka 7 adalah sisa dari pembagian terakhir yang tidak perlu kita bagi kembali dengan bilangan prima karena akan menghasilkan angka 1, dimana angka 1 jika dikalikan dengan bilangan lain hanya akan menghasilkan bilangan yang dikalikan tersebut.
Misal perkalian 1 x 7 adalah 7.
Jadi, sudah jelas bahwa pembagian akhir yang menghasilkan angka 1 tidak perlu dilanjutkan.
Perlu diketahui pula bahwa pembagian di atas dapat kita susun seperti bagan di bawah ini.
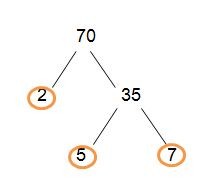
Bagan di atas disebut dengan pohon faktor.
Sedangkan, angka yang dilingkari merupakan bilangan prima sebagai pembagi, yaitu 2,5 dan 7.
Angka ini merupakan faktor prima.
Jika ditulis seperti ini 70=2x5x7, maka disebut faktorisasi prima.
Untuk mempermudah, di bawah ini diberikan daftar angka-angka yang termasuk bilangan prima.
Rumus Dan Cara Menentukan Bilangan Prima
Bilangan prima adalah bilangan yang bervariasi.
Namun, kita telah mengetahui bahwa 99% anggota bilangan prima adalah ganjil kecuali angka 2.
Ada beberapa cara untuk menentukannya.
Secara umum, kita dapat menentukan bilangan prima menggunakan ketentuan rumus berikut yang didasari dari sifat bilangan prima itu sendiri.
- Bilangan prima yang terdiri lebih dari 2 digit, tidak berakhiran angka 0 atau 5. Contoh : 10, 15, 20, 25 dst.
- Jumlah dari digit bilangan prima tidak berkelipatan 3. Maksudnya adalah seperti ini. Misalkan, ada bilangan 126. Maka jumlah dari penjumlahan digit tersebut 1+2+6=9. Angka 9 dapat dibagi 3, yaitu 126:3=42, 42:3=14. Sehingga bilangan 126 bukanlah bilangan prima.
Catatan : bilangan prima tidak ada yang negatif.
Cara lain untuk menentukan bilangan prima adalah dengan membuat kolom tabel.
Kita menggunakan angka 2, 3, 5 dan 7 sebagai patokan.
Dengan cara ini, kita dapat dipermudah dalam menemukan bilangan prima khususnya antara 1-100.
Untuk menentukan bilangan prima di atas 100, dianjurkan untuk menggunakan langkah yang telah dijelaskan sebelumnya.
Nah, berikut adalah cara jitu menentukan bilangan prima antara 1-100.
- Buatlah 100 kolom menggunakan tabel 10 x 10.
- Tandai angka 1 dengan tinta merah.
- Lalu, tandai angka yg habis dibagi 2 dengan tinta biru, yang habis dibagi 3 dengan kuning, yang habis dibagi 5 dengan hijau, dan yang habis dibagi 7 dengan ungu.
- Sisa angka yang tidak diwarnai adalah bilangan prima.
Di bawah ini adalah contoh penerapan warna pada tabel bilangan prima.
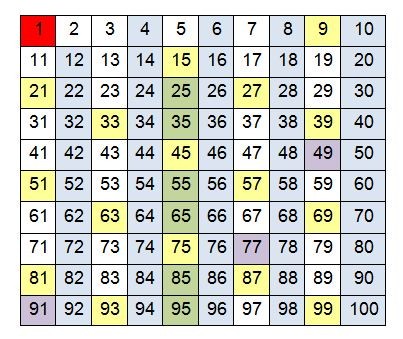
Bilangan Prima Terbesar
Secara ilmiah, tidak terdapat bilangan prima terbesar.
Hal ini juga telah dibuktikan oleh seorang ilmuwan matematika dari Yunani bernama Euclid.
Maksud dari tidak ada bilangan terbesar disini adalah karena bilangan prima itu tak terhingga, maka tidak ada bilangan terbesar, selalu ada bilangan terbesar dari yang terbesar.
Bilangan prima yang dicari adalah dalam bentuk bilangan prima Mersenne.
Apa itu Mersenne? Merupakan rumus 2p-1 untuk menuliskan bilangan prima.
Huruf p adalah lambang untuk bilangan prima, yaitu 2, 3, 5, 7 dst.
Sedangkan hasil dari rumus 2p-1 disebut bilangan prima Mersenne, dengan simbol Mp.
Kegiatan mencari bilangan prima terbesar ini sebenarnya sudah berlangsung sejak 500 tahun sebelum masehi.
Beberapa Mp yang telah ditemukan kala itu misalnya, 3, 7, 31, 127 dengan p = 2, 3, 5, 7 secara berurutan.
Jika dijabarkan maka akan seperti ini. Mp 3 = 22-1, Mp 7 = 23-1, Mp 31 = 25-1, dan Mp 127 = 27-1.
Untuk memudahkan, maka bilangan Mersenne tersebut dijuluki sesuai dengan bilangan primanya.
Menjadi, M2, M3 dst. Jumlah digit yang ditemukan masih sangat kecil dan dapat diperkirakan tanpa menggunakan mesin komputasi.
Pada tahun 1456, Banyak ilmuwan berlomba-lomba untuk mencari bilangan prima Mersenne ini.
Kegiatan ini dilakukan semata-mata untuk hobi di kalangan para ilmuwan.
Hingga tahun 1996, telah banyak ditemukan bilangan Mersenne ini, yaitu sejumlah 34 bilangan prima Mersenne.
Bilangan tersebut ditemukan oleh David Slowinski dan rekannya Paul Gage, tepatnya pada tanggal 03 September 1996.
Bilangan tersebut adalah 21.257.787-1, berjumlah 378.632 digit.
Lalu bilangan ini dijuluki M1.257.787.
Hobi ini semakin berkembang.
Organisasi bernama Great Internet Mersenne Prime Search yang disingkat GIMPS pun akhirnya dibentuk dan pada tahun yang sama untuk pertama kalinya GIMPS menemukan Mp ke-35 yaitu 21.398.269-1, yang lebih besar dengan julukan M1.398.269.
penemuan ini sudah menggunakan sistem komputasi.
Tak sampai disitu, hobi ini terus berkembang dan berlanjut dari generasi ke generasi hingga pada tanggal 07 Desember 2018 lalu, sudah ditemukan Mp yang ke-51, yaitu 282.589.933-1 dengan total digit adalah 24.862.048 dan dijuluki M82.589.933.
Penemuan bilangan ini tidak serta merta.
GIMPS dengan sangat senang hati memberikan reward berupa uang tunai sebesar 3000 dollar.
Untuk lebih lengkapnya mengenai daftar bilangan prima Mersenne dari awal hingga ke-51, kita bisa mengunjungi situ Mersenne di mersenne.org/primes/.
Bahkan, untuk saat ini, perlombaan masih berlanjut untuk menemukan Mp dengan jumlah 100 juta digit.
Tidak main-main, reward yang ditawarkan adalah 150.000 dolar atau setara 2 milyar.
Tertarik? Silahkan dicoba.
Bilangan Komposit
Ada gula ada semut, ada siang ada malam.
Bilangan prima ternyata memiliki teman yang berupa bilangan juga.
Bilangan tersebut disebut bilangan komposit.
Apa itu komposit?
Bilangan komposit dapat diartikan sebagai lawan dari bilangan prima.
Semua angka yang bukan bilangan prima dapat kita sebut bilangan komposit.
Yang termasuk bilangan komposit adalah 4, 6, 8 dst.
Ciri khas dari bilangan komposit ini adalah mereka memiliki faktor pembagi lebih dari 2.
Misal angka 4, bisa dibagi 2, 4 dan 1.
Nah, apakah 0 dan 1 serta angka negatif termasuk bilangan komposit? Tentu saja tidak termasuk.
Mengapa? Begini penjelasannya.
- Nol (0) memiliki faktor tak terhingga, dan bukan bilangan asli.
- Satu (1) hanya memiliki 1 faktor.
- Angka negatif bukan bilangan asli.
Untuk memudahkan kita memahami, coba simak tabel 3 perbedaan utama antara bilangan prima dan komposit di bawah ini.
| Ciri-ciri | Perbedaan | |
| Prima | Komposit | |
| Pembagi | Dapat dibagi 1 dan bilangan prima itu sendiri | Dapat dibagi 1, bilangan prima itu sendiri dan bilangan lain |
| Jumlah Faktor | 2 | Lebih dari 2 |
| Jenis | 99% ganjil kecuali angka 2 | Ada ganjil ada genap |
| 4 | 6 | 8 | 9 | 10 | 12 | 14 |
| 15 | 16 | 18 | 20 | 21 | 22 | 24 |
| 25 | 26 | 27 | 28 | 30 | 32 | 33 |
| 34 | 35 | 36 | 38 | 39 | 40 | 42 |
| 44 | 45 | 46 | 48 | 49 | 50 | 51 |
| 52 | 54 | 55 | 56 | 57 | 58 | 60 |
| 62 | 63 | 64 | 65 | 66 | 68 | 69 |
| 70 | 72 | 74 | 75 | 76 | 77 | 78 |
| 80 | 81 | 82 | 84 | 85 | 86 | 87 |
| 88 | 90 | 91 | 92 | 93 | 94 | 95 |
| 96 | 98 | 99 | 100 |
1. Temukan bilangan prima di bawah ini?
35
38
67
51
Jawab : c
2. Apa saja faktor prima dari 72?
Buatlah pohon faktor terlebih dahulu.
Jawab : 2 x 2 x 2 x 3 x 3
3. Tuliskan bilangan prima antara 32 dan 52.
Jawab : 37, 41, 43, 47
Tuliskan bilangan komposit antara 85 dan 95.
Jawab : 86, 87, 88, 90, 91, 92, 93, 94
4. Manakah yang merupakan bilangan komposit?
7
93
79
23
Jawab : 93
Sejarah Bilangan Prima

Bilangan prima ditemukan pertama kali oleh seorang ilmuwan di bidang matematika dari Yunani kuno bernama Euclid atau Eukleides.
Ini sekitar 325 sebelum masehi yang lalu.
Euclid menulis menulis sebuah buku berjudul “The Elements” yang di dalamnya juga dibahas mengenai bilangan prima. Euclid juga menyebutkan bahwa bilangan prima jumlahnya banyak sekali.
Di era selanjutnya, sekitar 276 sebelum masehi, Eratosthenes menemukan cara mudah untuk mencari bilangan prima.
Cara ini Ia sebut dengan sistem saringan karena menggunakan kolom-kolom angka yang kemudian dieliminasi dengan ketentuan tertentu, seperti mencoret angka yang habis dibagi 2, 3, 5 dan 7.
Pada tahun 1588, munculah bilangan Mersenne.
Bilangan ini ditemukan oleh biarawan Prancis bernama Marine Mersenne.
Ia membuat rumus 2p-1. Penemuan dilanjutkan oleh Fermat, pada tahun 1601 yang menyatakan bahwa rumus akan selalu menghasilkan bilangan prima, yang kemudian diperinci oleh Gauss pada tahun 1777.
Nah, itu tadi penjelasan menyeluruh mengenai bilangan prima.
Sangat mengasyikkan ya belajar matematika itu.
Yuk, tambah semangat belajarnya dan jangan lupa untuk mengulang pelajaran ya.
